TEMA 5: INFERENCIA SOBRE PROPORCIONES
Capitulo 2: Ejemplo
Comenzamos considerando en ejemplo sencillo que permite ilustrar las ideas básicas sobre inferencia sobre proporciones.
Disponemos de dos equipos nuevos de programadores recién contratados; se desea saber cuál de los dos equipos será más eficiente, es decir, acabará antes las tareas de programación que les asignamos. De las entrevistas y los curricula vitae se tiene ciertas sospechas de que A es mejor B, pero no se está seguro de cuánto mejor. Más aún, aunque A sea mejor puede ocurrir que para algunas tareas el equipo B concluya antes.
Sea A el suceso ``el equipo A concluye antes el próximo trabajo que le planteamos''. Podríamos asignar nuestra probabilidad de que ocurra A directamente, pero esto puede ser difícil y lo hacemos empleando los métodos ya estudiados. Para ello pensamos que el resultado de la prueba viene determinado por (o es asimilable a) la selección de una bola de una bolsa con bolas A y bolas B; la proporción de bolas A es la proporción de veces que A acabará antes. Si hay más bolas A, A será mejor. No se conoce tal proporción puesto que que se tiene incertidumbre sobre las habilidades del equipo A, por lo que se consideran varios modelos de bolsas.
Específicamente, supondré que hay 10 bolas en la bolsa, pudiendo ir el número de bolas de A de 0 a 10. Así, por ejemplo, si hay 8 bolas A, la proporción de bolas A será 0.8, y A será 4 veces más probable que acabe antes que B la próxima tarea que les asignemos. Supondremos que las capacidades de los equipos no cambiarán en el periodo de estudio. Sin embargo, nuestra percepción de sus capacidades sí puede cambiar al recibir información adicional.
Se asigna inicialmente nuestra probabilidad a priori sobre los distintos modelos según se indica en la siguiente tabla:
| Proporción de A's | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| Nuestra probabilidad | 0 | 0.02 | 0.03 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.15 | 0.05 | 0 |
Por ejemplo, decimos
![]()
porque aunque creemos que A es más eficiente no descartamos que pueda
concluir algunas tareas antes que A. A partir de tal asignación podemos
calcular nuestra probabilidad de que A sea mejor, que es
![]()
análogamente,
![]()
![]()
Un cálculo más interesante e importante es el de nuestra probabilidad de que A concluya la próxima tarea antes. Si conociese la composición correcta de la bolsa (o creyese conocerla), ésta sería la probabilidad indicada. Como no es así, empleamos la ley de probabilidad total: condicionamos y promediamos. En este caso concreto:
P(A acaba antes) = P(A
antes\ 0)![]()
![]() P
(0) + P(A antes\ 0.1)
P
(0) + P(A antes\ 0.1)![]()
![]() P
(0.1)+
P
(0.1)+ ![]()
![]()
![]()
![]()
![]()
![]() + P(A antes\ 1)
+ P(A antes\ 1)![]()
![]() P
(1) = 0
P
(1) = 0![]()
![]() 0
+ 0.1
0
+ 0.1![]()
![]() 0.02
+ 0.2
0.02
+ 0.2![]()
![]() 0.03
+ 0.3
0.03
+ 0.3![]()
![]() 0.05
+
0.05
+ ![]()
![]()
![]()
![]()
![]()
![]() + 1
+ 1![]()
![]() 0
= 0 + 0.002 + 0.006 + 0.015 +
0
= 0 + 0.002 + 0.006 + 0.015 + ![]()
![]()
![]()
![]()
![]()
![]() + 0 = 0.6.
+ 0 = 0.6.
Podemos plantearnos ahora la cuestión de que si lo que
nos interesaba era ![]()
![]() por qué no asignamos ésta directamente, en lugar de hacerlo a través del
argumento indirecto basado en los modelos de bolsas. La razón básica es que
no es probable que realicemos pruebas con ambos equipos que nos proporcionen
información (por ejemplo, les asignamos tres tareas, A acaba una de ellas
antes) con lo cual deberíamos actualizar nuestras probabilidades. Nuestra
intuición no es es especialmente buena al procesar esta información, cosa
que sí se consigue los tipos de modelos introducidos.
por qué no asignamos ésta directamente, en lugar de hacerlo a través del
argumento indirecto basado en los modelos de bolsas. La razón básica es que
no es probable que realicemos pruebas con ambos equipos que nos proporcionen
información (por ejemplo, les asignamos tres tareas, A acaba una de ellas
antes) con lo cual deberíamos actualizar nuestras probabilidades. Nuestra
intuición no es es especialmente buena al procesar esta información, cosa
que sí se consigue los tipos de modelos introducidos.
En efecto, para fijar ideas, supongamos que ponemos tres
tareas a los equipos A y B y B acaba antes dos de ellas (por ejemplo, para
simplificar la discusión, A acaba antes la primera y B las dos siguientes).
Se designa esta información mediante D y supongamos que vamos a plantearles
una nueva tarea; sea A, ahora el suceso ``A acaba antes que B''. Mis
probabilidades sobre los distintos modelos deberían haber cambiado, por
conocer D, lo que afectaría a mi probabilidad sobre A (que recordamos estaba
alrededor de 0.6). De hecho, deberíamos esperar que fuera menor que 0.6, pues
D nos sugiere que B parece mejor de lo que, en principio creíamos. Nuestro
objetivo es, por tanto, calcular ![]()
![]() De nuevo se aplica la fórmula
de
probabilidad total.
De nuevo se aplica la fórmula
de
probabilidad total.
Nota: El método general, que ya fue desarrollado era
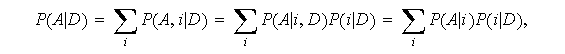
si ocurre como en el caso del ejemplo, que
![]()
Entonces,
![]()
Se puede observar que las probabilidades ![]()
![]() no quedan afectadas por la nueva información, pero lo que sí cambian son las
probabilidades
no quedan afectadas por la nueva información, pero lo que sí cambian son las
probabilidades ![]()
![]()
Para calcular las probabilidades a posteriori de cada uno de los modelos se aplica la regla de Bayes
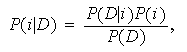
con
![]()
Recordemos que las ![]()
![]() se denominan probabilidades a priori, las
se denominan probabilidades a priori, las ![]()
![]() se denominan probabilidades a posteriori y
se denominan probabilidades a posteriori y ![]()
![]() verosimilitudes (o probabilidades de los datos supuesto cierto el modelo
verosimilitudes (o probabilidades de los datos supuesto cierto el modelo ![]()
![]() ).
En este caso concreto (D = A, B, B) las verosimilitudes son
).
En este caso concreto (D = A, B, B) las verosimilitudes son
![]()
Aplicando, entonces, la fórmula de Bayes tenemos la transformación de probabilidades a priori a probabilidades a posteriori que da la tabla:
| Modelo |
Prob. a
priori |
Prob. a
posteriori |
| 0 | 0 | 0 |
| 0.1 | 0.02 | 0.02 |
| 0.2 | 0.03 | 0.04 |
| 0.3 | 0.05 | 0.09 |
| 0.4 | 0.10 | 0.17 |
| 0.5 | 0.15 | 0.22 |
| 0.6 | 0.20 | 0.22 |
| 0.7 | 0.25 | 0.18 |
| 0.8 | 0.15 | 0.06 |
| 0.9 | 0.05 | 0.01 |
| 1 | 0 | 0 |
Por ejemplo,para ![]()
![]()

Como ![]()
![]() resulta que
resulta que
![]()
A partir de las probabilidades a posteriori podemos calcular, por ejemplo, la probabilidad de que A sea mejor, dados los datos, que sería
![]()
(se puede comparar con la probabilidad inicialmente calculada que era de
0.65).
Sin embargo, la probabilidad que más nos interesa es ![]()
![]() que será, como hemos indicado
que será, como hemos indicado
![]()
Se ha producido, pues, una reducción en la probabilidad (de 0.6 a 0.52), pero no es muy grande, puesto que los datos no son muy concluyentes.
Este ejemplo resume la esencia de las tareas a realizar en un problema estadístico. En lo que sigue se aplicará un esquema similar.
