TEMA 3: CÁLCULO DE PROBABILIDADES
Capitulo 4: Definición axiomática de probabilidad
Probabilidad condicionada e independencia de sucesos
A partir de ahora, supondremos que las probabilidades que se emplean son medidas de los grados de creencia de un individuo.En numerosas ocasiones, tendremos que modelizar una situación en la que se dispone de información adicional, debiendo condicionarse a sucesos o circunstancias. De hecho, en Estadística este será el letit-motiv básico: debemos procesar información nueva, o lo que es lo mismo, condicionar a una nueva información. Formalmente, suponemos que estamos interesados en un suceso A, hemos asignado P(A) y nos informan de que ha ocurrido B y queremos saber cómo cambian mis creencias sobre A
Obviamente, en algunos casos no cambiarán tales creencias. Por ejemplo, si nos dicen que A = E (esto es, no nos dicen nada nuevo, no aportan información), P(B) no debe cambiar. En la mayor parte de los casos, sin embargo, el aporte de nueva información modifica la probabilidad.
El concepto básico para modelizar tales ideas es la probabilidad condicionada P(B|A). Su definición es la siguiente.
Sea B Ì
E un suceso
aleatorio de probabilidad no nula, P(B) > 0 . Para
cualquier otro suceso A Ì
E se llama probabilidad condicionada de A respecto de B a la
cantidad que representamos mediante
P(A|B) y se calcula como
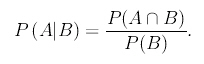
Observación:
Obsérvese que según la definición de la probabilidad condicionada, se puede escribir la probabilidad de la intersección de dos sucesos de probabilidad no nula como![]()
o sea, la probabilidad de la intersección de dos sucesos, es la probabilidad de uno cualquiera de ellos, multiplicada por la probabilidad del segundo sabiendo que ha ocurrido el primero.
Si entre dos sucesos no existe ninguna relación cabe esperar que la expresión sabiendo que no aporte ninguna información. De este modo introducimos el concepto de independencia de dos sucesos A y B como:
Esta relación puede ser escrita de modo equivalente: dados dos sucesos de probabilidad no nula (de manera que P(A) ¹ 0 ¹ P(B)) diremos que A es independiente de B si y sólo si P(A) = P(A|B) ó equivalentemente P(B) = P(B|A).
Así, se dice que dos experimentos son independientes si los resultados de uno son independientes de los del otro, para cualquier par de resultados que se escoja. Las definiciones se extienden, de forma inmediata, al caso de independencia de tres o más sucesos o experimentos.