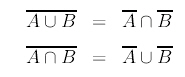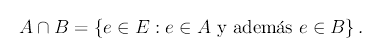TEMA 3: CÁLCULO DE PROBABILIDADES
Capitulo 3: Operaciones básicas con sucesos aleatorios
Al ser los sucesos aleatorios nada más que subconjuntos de un conjunto E, espacio muestral, podemos aplicar las conocidas operaciones con conjuntos, como son la unión, intersección y diferencia:
| Unión: Dados dos
sucesos aleatorios , A,B Ì
E , se denomina suceso unión de A y B al conjunto formado por
todos los sucesos elementales
que pertenecen a A o bien pertenecen a B
incluyendo los que están en ambos simultáneamente, es decir |
![]()
Como ejemplo, tenemos que la unión de un suceso cualquiera con su complementario es el suceso seguro.Volviendo al ejemplo del lanzamiento de un dado, si
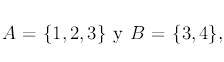
, el suceso unión de A y B es
| Intersección: Dados dos sucesos aleatorios , |
![]()
se denomina suceso intersección de A y B al conjunto formado por todos los sucesos elementales que pertenecen a A y B a la vez, es decir,
A veces por comodidad se omite el símbolo Ç para denotar la intersección de conjuntos, sobre todo cuando el número de conjuntos que intervienen en la expresión es grande. En particular, podremos usar la siguiente notación como equivalente a la intersección:
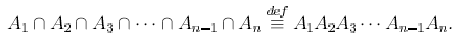
Un ejemplo de intersección es la de un suceso aleatorio cualquiera, A É E, con su complementario, que es el suceso imposible.Volviendo al ejemplo del dado, si
![]()
el suceso intersección de A y B es:
![]()
|
Diferencia: Dados dos sucesos aleatorios
A,B Ì
E, se llama
suceso diferencia de A y B, y se representa mediante A/B, o bien A-B, al suceso formado por todos los sucesos elementales que pertenecen a A, pero no a B: |
Por ejemplo, si
Obsérvese que el suceso contrario de un suceso A, puede escribirse como la diferencia del suceso seguro menos éste, o sea,
|
Diferencia simétrica: Si A,B Î
E , se denomina suceso diferencia simétrica
de A y B, y se representa mediante A D B al suceso aleatorio formado por todos los sucesos elementales que pertenecen a A y no a B, y los que están en B y no en A: |
Por ejemplo, si
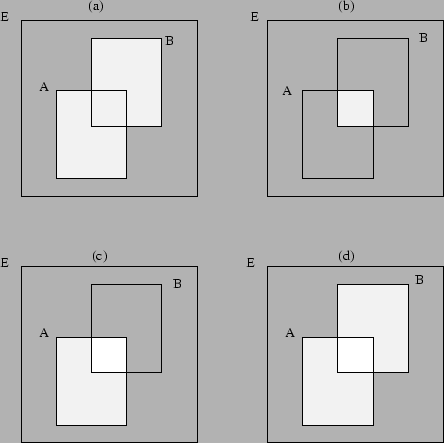
Figura 4.2. Dados dos sucesos aleatorios A,B E se representa: en (a) A È B; en (b) A Ç B; en (c) A - B; en (d) A D B
Hay ciertas propiedades que relacionan la unión, intersección y suceso contrario, que son conocidas bajo el nombre de Leyes de Morgan: