TEMA 3: CÁLCULO DE PROBABILIDADES

Capitulo 2: Experimentos y sucesos aleatorios

Se dice que un experimento es aleatorio si se verifican las siguientes condiciones:

	Se puede repetir indefinidamente, siempre en las mismas condiciones;
	Antes de realizarlo, no se puede predecir el resultado que se va a obtener;
	El resultado que se obtenga, e, pertenece a un conjunto conocido previamente de resultados posibles. A este conjunto, de resultados posibles, lo denominaremos espacio muestral y lo denotaremos normalmente mediante la letra E. Los elementos del espacio muestral se denominan sucesos elementales.

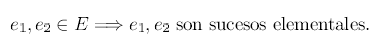
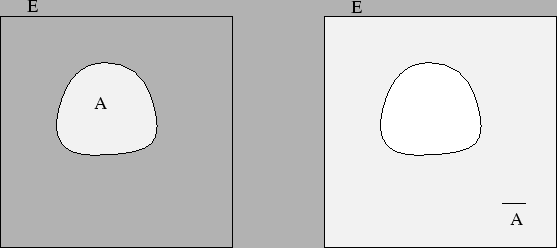
Cualquier subconjunto de E será denominado suceso aleatorio, y se denotara normalmente con las letras A,B,...

Se puede observar que los sucesos elementales son sucesos aleatorios compuestos por un sólo elemento. Por supuesto los sucesos aleatorios son más generales que los elementales, ya que son conjuntos que pueden contener no a uno sólo, sino a una infinidad de sucesos elementales (y también no contener ninguno). Sucesos aleatorios que aparecen con gran frecuencia en el cálculo de probabilidades son los siguientes:

Suceso seguro: Es aquel que siempre se verifica después del experimento aleatorio, es decir, el mismo E

Suceso imposible: Es aquel que nunca se verifica como resultado del experimento aleatorio. Como debe ser un
subconjunto de E, la única posibilidad es que el suceso imposible sea el conjunto vacío:

Suceso contrario a un suceso A: También se denomina complementario de A y es el suceso que se verifica si,
como resultado del experimento aleatorio, no se verifica A. Se acostumbra a denotar con el símbolo

Figura 4.1. Representación gráfica de un suceso aleatorio A Ì E y de su suceso contrario