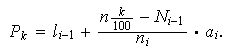TEMA 2: MEDIDAS DESCRIPTIVAS

    Para una variable discreta, se define el percentil de orden , como la observación, , que deja por debajo de sí el de la muestra. Esta definición es semejante a la de la mediana, pues como consecuencia de la definición, es evidente que

   Por su propia naturaleza, el percentil puede estar situado en cualquier lugar de la distribución, por lo que no se puede considerar como una medida de tendencia central, sino más bien de posición .

    Los cuartiles, , son un caso particular de los percentiles. Hay 3, y se definen como:

Primer Cuartil: .

Segundo Cuartil: . Es equivalente a la Mediana.

Tercer Cuartil: .

    De forma análoga se pueden definir los deciles como los valores de la variable que dividen a las observaciones en 10 grupos de igual tamaño. Más precisamente, definimos como:

donde .

    Los percentiles (que incluyen a la mediana, cuartiles y deciles) también son denominados estadísticos de posición.

       Al igual que en el caso del cálculo de la mediana cuando las variables son variables continuas y están agrupadas en intervalos, el cálculo de estos estadísticos de posición es más complicado. Se supone que el valor se encuentra en un intervalo dado y hay que determinar el punto que deja exactamente el porcentaje correspondiente de observaciones a un lado y al otro. Mediante un argumento geométrico se deduce también que el percentil es el valor tal que