TEMA 5: INFERENCIA SOBRE PROPORCIONES

    Se considera ahora una extensión del ejemplo introductorio. En él hemos considerado como modelo de referencia bolsas con 10 bolas y dos símbolos A ó B. Escoger 10 bolas fue arbitrario; podríamos haber escogido bolsas con 15 bolas ó 37 ... De hecho, en este ejemplo, es plausible cualquier proporción (entre 0 y 1) por lo que en lugar de mantener un numero finito de modelos deberíamos considerar un número infinito de modelos. Para ello emplearemos el modelo beta-binomial.

    La situación que consideramos es la misma que en el enunciado inicial. Se desea aprender y proporcionar información sobre , la proporción de casos que se produce cierto fenómeno, pudiéndose dar sólo dos resultados. Disponemos de creencias iniciales sobre que se mueve entre 0 y 1.

    En el capítulo previo se describió la familia de distribuciones beta como suficientemente flexible para modelizar creencias sobre proporciones. Se tienen numerosas formas posibles de la función de densidad beta

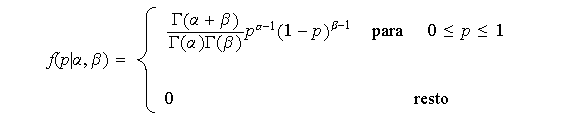
Se tiene, además, que

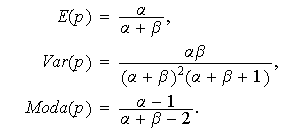
    Por ejemplo, para se tiene la distribución uniforme que modeliza la ignorancia acerca de cuando se concentra la probabilidad hacia la derecha, y a la inversa en el caso contrario. Cuanto mayores son y la densidad está más concentrada.

    Suponemos, además, que tenemos acceso a información adicional a través de un experimento que consiste en observar casos independientes, registrándose el número de casos favorables que se presentan. La verosimilitud (o el modelo) es, en este caso, binomial, teniéndose

para

    Se realiza, por tanto, el experimento y supongamos que se producen éxitos. Actualizamos, entonces nuestras creencias sobre aplicando la fórmula de Bayes.

    Nota: Se puede considerar el teorema de Bayes en los casos continuo y discreto. Aquí se tiene un caso mixto, discreto () y continuo (), pero la fórmula se preserva, como es de esperar.

Se tiene

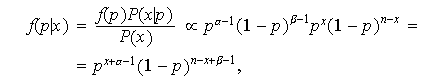
siendo y para

    Resulta, por tanto, que la distribución a posteriori de sigue una beta de parámetros y Emplearemos tal distribución para resolver los problemas típicos que se presentan en Inferencia.