TEMA 4: VARIABLES ALEATORIAS
Capitulo2: Variables Aleatorias Discretas. Distribuciones Discretas
Distribución Binomial
Se utiliza la distribución binomial para modelizar el número de veces que se da un resultado al realizar varias pruebas idénticas e independientes de un experimento con dos resultados posibles. Tales situaciones son muy abundantes, como indican estos ejemplos informáticos:
 |
En el desarrollo de interfaces inteligentes y de modelos de recuperación de la información, podemos considerar que al presionar una tecla, la persona puede teclear o no el carácter deseado. |
|
En el estudio de un sistema de disco, podemos considerar que un acceso a disco puede concluir con la recuperación o no del registro requerido. |
|
En el estudio del envío de trabajos a un sistema, podemos suponer el tiempo partido en trozos y considerar que en cada trozo puede producirse, o no, una llegada. |
Las hipótesis específicas que se hacen son:
|
Se consideran |
|
El experimento tiene dos resultados posibles: éxito o fracaso. |
|
La probabilidad |
El espacio muestral del experimento es el conjunto 
de 
-uplas
(éxito o fracaso). La variable 
de interés es el número de éxitos obtenidos en esas 
pruebas.
Entonces, se dice que 
tiene distribución binomial de parámetros 
y 
y se escribe como 
siendo la distribución
Forma de la Distribución Binomial
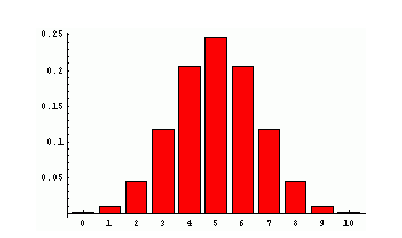
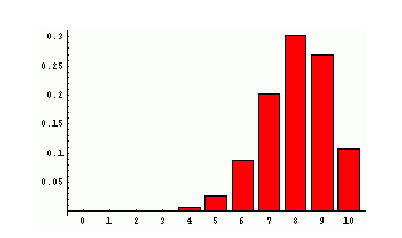
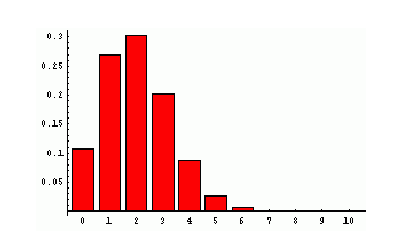
Forma de la distribución Binomial en función de p.
Es interesante remarcar la forma de la distribución binomial en función de 
 |
Cuando |
|
|
|
Cuando |
|
|
|
Cuando |
|
|
