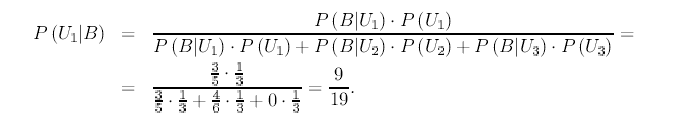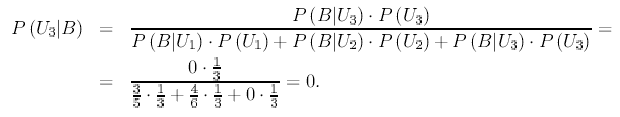TEMA 3: CÁLCULO DE PROBABILIDADES
Capítulo 5: Ciertos Teoremas Fundamentales del Cálculo de Probabilidades.
Teorema de Bayes. Ejemplo
Se tienen tres urnas. Cada una de ellas contiene un número diferente de bolas blancas y rojas:| Primera urna, U1: 3 bolas blancas y 2 rojas; | |
| Segunda urna, U2: 4 bolas blancas y 2 rojas; | |
| Tercera urna, U3: 3 bolas rojas. |
Si el resultado del experimento es que ha salido una bola blanca, ¿cuál es la probabilidad de que provenga de la primera urna? Calcular lo mismo para las otras dos urnas.
Solución
Vamos a representar en un esquema los datos de que disponemos:
|
|
En este caso U1, U2 y U3
forman un sistema exhaustivo y mutuamente excluyente
(la bola resultado debe provenir de una
de esas tres urnas y de una sólo de ellas), por tanto es posible aplicar el teorema
de Bayes:
|
|
|
|