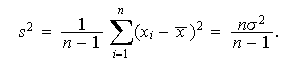TEMA 2: MEDIDAS DESCRIPTIVAS

Capítulo 7. Medidas de Variabilidad o Dispersión

Variación y Desviación Estándar. Observaciones.

La varianza y la desviación estándar tienen las siguientes propiedades:

	Ambas son sensibles a la variación de cada una de las puntuaciones, es decir, si una puntuación cambia, cambia con ella la varianza ya que es función de cada una de las puntuaciones.
	La desviación típica tiene la propiedad de que en el intervalo se encuentran por lo menos el $75\%$ de las observaciones (es el llamado teorema de Thebycheff). Incluso si tenemos muchos datos y estos provienen de una distribución normal, podremos llegar al $95\%$ de las observaciones.
	No es recomendable el uso de ellas, cuando tampoco lo sea el de la media como medida de tendencia central, por ejemplo, en datos nominales.

Un principio general de la inferencia estadística afirma que si pretendemos calcular de modo aproximado la varianza de una población a partir de la varianza de una muestra suya, se tiene que el error cometido es generalmente más pequeño, si en vez de considerar como estimación de la varianza de la población, a la varianza muestral consideramos lo que se denomina cuasivarianza muestral, $s^{2},$ que se calcula como la anterior, pero cambiando el denominador por :

MATH