TEMA 2: MEDIDAS DESCRIPTIVAS
Capítulo 7. Medidas de Variabilidad o Dispersión
Variación y Desviación Estándar. Ejemplo.
Calcular la varianza y desviación típica de las siguientes cantidades medidas en metros: 3,3,4,4,5
Solución:
Para calcular dichas medidas de dispersión es necesario calcular previamente el valor con respecto al cual vamos a medir las diferencias. Éste es la media:
![]()
La varianza es:
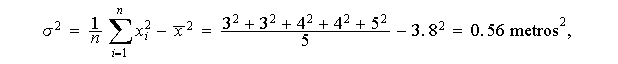
y la desviación
estándar es ![]()
![]() metros.
metros.
Las siguientes propiedades de la varianza (respectivamente, desviación típica) son importantes a la hora de hacer un cambio de origen y escala a una variable. En primer lugar, la varianza (respectivamente desviación típica) no se ve afectada si al conjunto de valores de la variable se le ańade una constante. Si además cada observación es multiplicada por otra constante, en este caso la varianza cambia con relación al cuadrado de la constante (respectivamente la desviación típica cambia con relación al valor absoluto de la constante).