TEMA 2: MEDIDAS DESCRIPTIVAS

Capítulo 2. Medidas de Centralización.

Media Aritmética.

La media aritmética de una variable estadística es la suma de todos sus posibles valores, ponderada por las frecuencias de los mismos. Es decir, si la tabla de valores de una variable es

	$n_{i}$	$f_{i}$
$x_{1}$	$n_{1}$	$f_{1}$

$x_{k}$	$n_{k}$	$f_{k}$

la media es el valor que podemos escribir de las siguientes formas equivalentes:

MATH

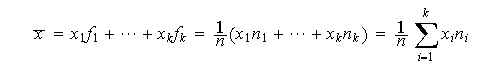
Si los datos no están ordenados en una tabla, entonces

Hemos supuesto implícitamente en la definición de media que tratábamos con una variable discreta. Si la variable es continua y se utilizan tablas con intervalos se tienen que cambiar los valores de $x_{i}$ por las marcas de clase correspondientes $c_{i}$ . En general, la media aritmética obtenida a partir de las marcas de clase $c_{i}$ , diferirá de la media obtenida con los valores reales, $x_{i}$ . Es decir, habrá una perdida de precisión que será tanto mayor cuanto mayor sea la diferencia entre los valores reales y las marcas de clase, o sea, cuanto mayores sean las longitudes $a_{i}$ , de los intervalos.