TEMA 2: MEDIDAS DESCRIPTIVAS
Capítulo 8. Asimetría y Apuntamiento
Coeficiente de Asimetría.
Para saber si una distribución de frecuencias es simétrica, hay que precisar con respecto a qué. Un buen candidato es la mediana, ya que para variables continuas, divide al histograma de frecuencias en dos partes de igual área. Podemos basarnos en ella para, de forma natural, decir que una distribución de frecuencias es simétrica si el lado derecho de la gráfica (a partir de la mediana) es la imagen por un espejo del lado izquierdo (figura 2.7).
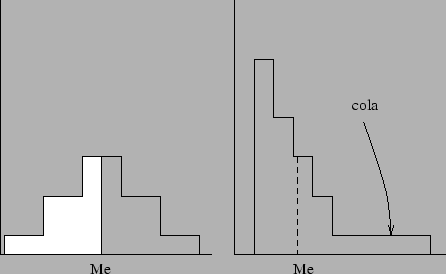
Figura 2.7: Distribuciones de frecuencias simétricas y asimétricas
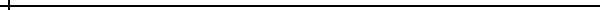
Observaciones
Si una variable es continua simétrica y unimodal, coinciden la media, la mediana y la moda.
Dentro de los tipos de asimetría posible, se pueden destacar los dos fundamentales (figura 2.8):
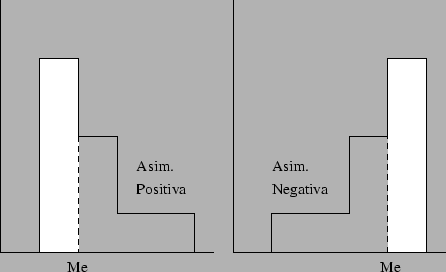
Figura 2.8: Asimetría positiva y asimetría negativa
Asimetría positiva: Si las frecuencias más altas se encuentran en el lado izquierdo de la media, mientras que en la parte derecha hay frecuencias más pequeñas (en la cola).
Asimetría negativa: Cuando la cola está en el lado izquierdo.
Se puede definir un coeficiente
de asimetría. Previamente, se tiene que definir el momento de
orden 
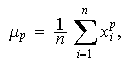
y el el momento central de orden 
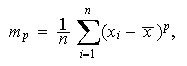
entonces el coeficiente de asimetría se define como
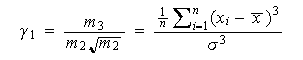
Apoyándonos en este índice, se dice que hay asimetría
positiva si 
,
y que la asimetría es negativa si 
Se puede observar que es un índice adimensional, sin unidades de medida. Por otro lado, sucede que diferencias importantes entre la media y la moda o la media y la mediana indican asimetría.