TEMA 6: INFERENCIA PARA MEDIAS. MODELOS NORMALES
Capitulo 10: Comparación de Varias Medias
Ejemplo
Supongamos que en el ejemplo anterior comparamos el
grupo T1 con el grupo T3. Como
distribución a priori supondremos en ambos grupos ![]()
![]()
![]()
![]() no es conocida y la sustituimos por
no es conocida y la sustituimos por ![]()
![]() sin corrección, pues los tamaños muestrales son suficientemente grandes.
sin corrección, pues los tamaños muestrales son suficientemente grandes.
Los estadísticos relevantes son
Con una
media a priori ![]()
![]() y una desviación
estándar a priori
y una desviación
estándar a priori ![]()
![]() queda
queda
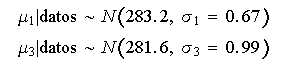
y
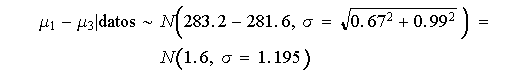
Tenemos
![]()
Si calculamos el intervalo de probabilidad a posteriori del 95%, se tiene que
![]()
de modo que ![]()
![]()
Así pues, hay cierta evidencia de que T1 aumenta el rendimiento, sin embargo, 0 está en el intervalo del 95%. Por tanto parece que no hay mucha diferencia entre las medias de ambas poblaciones.
Ahora combinamos los grupos T2 y T3
| T1 | T2+T3 | |
| Nº | 266 | 267 |
| Media | 283.3 | 280.52 |
| Desv. Típica | 11.1 | 12.6 |
Se tiene que
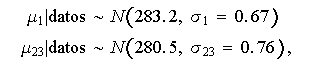
independientes, luego
![]()
Se tiene que ![]()
![]() y un intervalo del 95% es
y un intervalo del 95% es ![]()
![]() de modo que el 0 no está incluido dentro.
de modo que el 0 no está incluido dentro.
Parece, pues, que hay evidencia de que el tratamiento T1 aumenta el rendimiento.