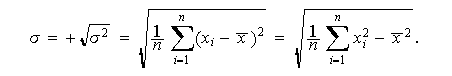TEMA 2: MEDIDAS DESCRIPTIVAS
Capítulo 7. Medidas de Variabilidad o Dispersión
Variación y Desviación Estandar.
Si las desviaciones con respecto a la
media las
consideramos al cuadrado, 
de nuevo obtenemos que todos los sumandos tienen el mismo signo (positivo). Esta
es además la forma de medir la dispersión de los datos de forma que sus
propiedades matemáticas son más fáciles de utilizar. Se pueden definir,
entonces, dos estadísticos fundamentales: La varianza y la desviación estándar
(o típica).
La varianza, 
se define como la
media de las diferencias cuadráticas de 
puntuaciones con respecto a su
media aritmética, es decir
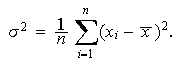
Una fórmula equivalente para el cálculo de la varianza está basada en lo siguiente:
La varianza no tiene la misma magnitud que las
observaciones (ej. si las observaciones se miden en metros,
la varianza lo hace en metros
2)
Si queremos que la medida de dispersión sea de la misma dimensionalidad que las
observaciones bastará con tomar su raíz cuadrada. Por ello se define la desviación
estándar, 
,
como
