TEMA 5: INFERENCIA SOBRE PROPORCIONES
Capitulo 3: El Modelo Beta-Binomial.
Ejemplo
Un distribuidor de cierto prestigio anuncia que el 95% de sus ordenadores no debe recibir inspección durante el año de garantía. Se modelizan las creencias sobre la proporción de ordenadores que no requieren reparación durante la garantía de esa marca mediante una
Se observa que si
entonces
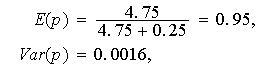
con lo que nos fiamos, en principio, mucho del distribuidor.
Debido a la aparente calidad, compramos 20 ordenadores, de los cuales 12 requieren reparación durante el año de garantía. Nuestra distribución a posteriori sobre la proporción es
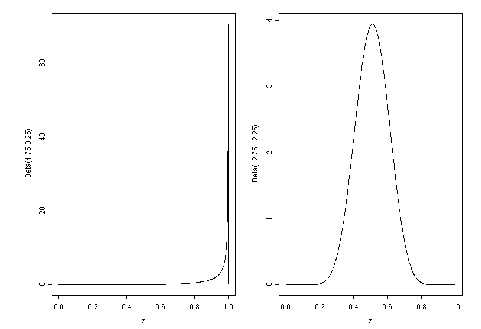
La figura muestra las distribuciones a priori y a posteriori.
|
|
Calcular:
-
Realizar el contraste de hipotesis
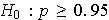frente a 
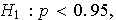que se correspondería con contrastar el anuncio. -
Predecir la probabilidad de que el proximo ordenador que compremos no deba repararse en periodo de garantia.
Solución
Estimadores puntuales.
Algunos valores que resumen la distribución a posteriori son:
Mediana a posteriori: 0.5102709 (en Splus:
qbeta(0.5,12.75,12.25)).
Estimación por intervalos:
Un intervalo de probabilidad 0.95 es
En Splus:
p <- c(0.025,0.975)
qbeta(p,12.75,12.25)Obteniéndose
Contraste de Hipótesis:
Contrastamos la hipótesis
Como, al considerar la orden en Splus,
pbeta(0.95,12.75,12.25), se obtiene 1, entonces se tiene que
por lo que los datos sugieren que el distribuidor está exagerando.
Predicción:
La probabilidad de que el siguiente ordenador que adquiramos no deba repararse en periodo de garantía es igual a la media a posteriori
