TEMA 5: INFERENCIA SOBRE PROPORCIONES
Capitulo 3: El Modelo Beta-Binomial.
Contraste de Hipótesis.
En muchas ocasiones se está interesado en un modelo
específico o subconjuntos de modelos que denominamos hipótesis
nula (
)
frente al resto de modelos que se denominan hipótesis
alternativa (
).
Por ejemplo, podemos contrastar
frente a
o podemos contrastar
frente a
Contrastar 
frente a 
significa calcular la probabilidad a posteriori de cada una de las hipótesis
y quedarse con la hipótesis más probable.
En el segundo ejemplo propuesto se calcularía
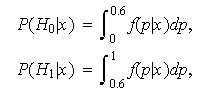
y se diría que los datos apoyan 
(frente a 
)
si
(o equivalentemente, 
).
El primer ejemplo es algo más delicado, pues 
,
al ser una distribución continua. Una solución rigurosa requiere cálculos más
sofisticados. Alternativamente, se puede esperar que la hipótesis puntual es,
de hecho, una aproximación a 
y proceder como antes. Si se pueden determinar 
y 
,
el problema quedaría resuelto.
También, como alternativa, se puede calcular un
intervalo 
de probabilidad 
centrado en la media a posteriori de 
y si 
decir que hay evidencia a favor de la hipótesis nula y, en otro caso, que hay
evidencia a favor de la hipótesis alternativa.
