TEMA 2: MEDIDAS DESCRIPTIVAS
Capítulo 7. Medidas de Variabilidad o Dispersión.
Desviación Media.
Se define la desviación media como la
media de las
diferencias en valor absoluto de los valores de la variable a la
media, es
decir, si tenemos un conjunto de 
observaciones, 
,
entonces
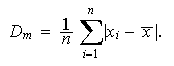
Como se observa, la desviación media guarda las mismas dimensiones que las observaciones. La suma de valores absolutos es relativamente sencilla de calcular, pero esta simplicidad tiene un inconveniente: desde el punto de vista geométrico, la distancia que induce la desviación media en el espacio de observaciones no es la natural (no permite definir ángulos entre dos conjuntos de observaciones). Esto hace que no sea muy conveniente trabajar con ella cuando se considera Inferencia Estadística.
Nota: Como forma de medir la dispersión de los datos se
tiene que descartar 
,
pues esa suma vale 
,
ya que las desviaciones con respecto a la
media se pueden compensan unas con
otras al haber términos en esa suma que son de signos distintos.
