TEMA 3: CÁLCULO DE PROBABILIDADES
Capitulo 4: Definición axiomática de probabilidad
Interpretación frecuentista de la probabilidad
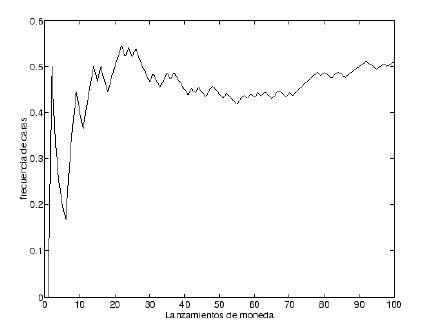
Un concepto más general de probabilidades es el frecuentista. Se aplica a experimentos que se pueden repetir indefinidamente bajo condiciones similares, adoptándose la hipótesis implícita de que las frecuencias relativas se estabilizan al repetirse el experimento.Por ejemplo, en la Figura 4.3 se presenta la evolución de la frecuencia relativa del número de caras obtenido en el lanzamiento de una moneda en 100 ocasiones (simulado por un ordenador). En principio la evolución de las frecuencias relativas es errática, pero a medida que el número de tiradas aumenta, tiende a lo que entendemos por probabilidad de cara.
|
|
Figura 4.3: Convergencia a 1/2 de la frecuencia relativa del número de caras obtenido en lanzamientos sucesivos de una moneda (simulación en ordenador).
Supongamos, en general, que un suceso A ocurre An veces
en n repeticiones del experimento. Resultaría, entonces, la definición
frecuentista de la probabilidad de A como

|
|
Se observa que no es posible, sin embargo, hablar de una sucesión infinita de repeticiones por lo que, en la práctica hablaremos de sucesiones largas:
La frecuencia a largo plazo de un suceso es la fracción de tiempo que ocurre tal suceso en una sucesión larga de ensayos.
Por ejemplo, si se tira un dado 10000 veces y se obtiene 1510 veces el 6, se puede decir que la probabilidad de obtener 6 al tirar ese dado es de 0.15. O, si en una UCI infantil ha habido 623 ingresos, de 3200, con la enfermedad A, puedo decir que la probabilidad de que ingrese un niño con la enfermedad A será de 623/3200.
Obviamente, si el número de ensayos es pequeño, carece de sentido emplear este concepto. Por ejemplo, si tiro un dado y no aparece ninguna vez el 4, en 5 tiradas, debería estimar la probabilidad de que aparezca un 4 en la próxima tirada mediante 0/5 (lo cual es absurdo).
Otras veces los experimentos aleatorios no pueden ser realizados, como es el caso de calcular la probabilidad de morir jugando a la ruleta rusa con un revólver: no es posible (o no se debe) calcular esta probabilidad repitiendo el experimento un número indefinidamente alto de veces para aproximarla mediante la frecuencia relativa.