TEMA 3: CÁLCULO DE PROBABILIDADES
Capitulo 4: Definición axiomática de probabilidad
Para hacer una definición rigurosa de la probabilidad, necesitamos precisar ciertas leyes o axiomas que debe cumplir una función de probabilidad. Intuitivamente, estos axiomas deberían implicar, entre otras, las siguientes cuestiones, que son lógicas en términos de lo que se puede esperar de una función de probabilidad:| La probabilidad sólo puede tomar valores comprendidos entre 0 y 1 (no
puede haber sucesos cuya probabilidad de ocurrir sea del 200% ni del -5%); |
|
| La probabilidad del suceso seguro es 1, es decir, el 100%; | |
| La probabilidad del suceso imposible debe ser 0; | |
| La probabilidad de la
intersección de dos sucesos debe ser menor o igual
que la probabilidad de cada uno de los sucesos por separado,
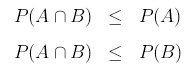 |
|
| La probabilidad de la
unión
de sucesos debe ser mayor o igual que la de
cada uno de los sucesos por separado,
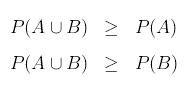
|
Más aún, si los sucesos son disjuntos (incompatibles) debe ocurrir que
| La probabilidad del
Suceso contrario a un suceso A
de A, debe valer |
![]()
En las últimas líneas se han esbozado ciertas propiedades que debería cumplir una función que se comporte como la probabilidad. Hemos de tener en cuenta entonces que siguiendo esos puntos:
- La función de probabilidad debe calcularse sobre subconjuntos de E. No es estrictamente necesario que sean todos, pero sí es necesario que si se puede calcular sobre un conjunto, lo pueda ser también sobre su complementario, y que si se puede calcular sobre dos conjuntos A y B , también se pueda calcular sobre su unión y su intersección. Para ello, introduciremos el concepto de s-álgebra de sucesos, que será una clase de subconjuntos de E sobre los que podamos aplicar las reglas de la probabilidad.
- Entre las leyes que debe cumplir una función de probabilidad y que hemos descrito antes, hemos observado que algunas son redundantes, ya que se pueden deducir de las demás. Con la definición axiomática de la probabilidad, pretendemos dar el menor conjunto posible de estas reglas, para que las demás se deduzcan como una simple consecuencia de ellas.
