TEMA 3: CÁLCULO DE PROBABILIDADES
Capitulo 4: Definición axiomática de probabilidad
Concepto axiomático de probabilidad
Dado un espacio muestral E, y una s-álgebra de sucesos A sobre él, diremos que P es una probabilidad sobre A si se verifica lo siguiente (axiomas):| Axioma 1 La probabilidad es una función definida sobre
A y que sólo toma valores positivos comprendidos entre 0 y 1. |

| Axioma 2. La probabilidad del suceso seguro es 1: |
![]()
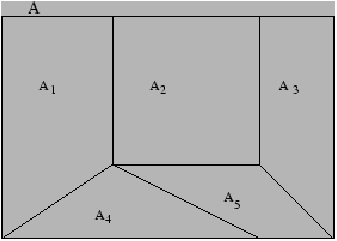
| Axioma 3. La probabilidad de la
unión
numerable de sucesos
disjuntos es la suma de sus probabilidades (figura 4.4): |
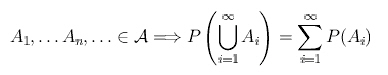
NOTA: El tercer axioma de probabilidad indica que si
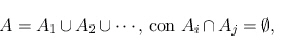
entonces
![]()
|
|
Observación:
La introducción de la definición de experimento aleatorio puede parecer innecesaria a primera vista, ya que es una clase formada por subconjuntos de E que verifican ciertas propiedades relativas a la complementariedad y a las uniones finitas que ya verifica de antemano el conjunto denominado partes de E,P(E), formado por todos los subconjuntos de E. Cuando el conjunto E de los posibles resultados de un experimento aleatorio sea finito, normalmente consideraremos como s-álgebra de sucesos al conjunto P(E). Esto ocurre cuando por ejemplo realizamos el experimento aleatorio de lanzar un dado:![]()
![]()
![]()
lo que por supuesto incluye a los puntos de R+, ya que por
ejemplo
![]()
Este tipo de conjuntos (los intervalos) son los que interesan en la práctica por lo que se considera el siguiente convenio:
No haremos en general referencia a la s-álgebra de sucesos más que cuando sea estrictamente necesario. De este modo cuando a partir de ahora se diga A Ì E , nos referiremos ímplicitamente a que A Î A donde A es una s-álgebra de sucesos asociado a E y sobre la que se ha definido la función de probabilidad.
Si el espacio muestral es finito o infinito numerable, entenderemos que el s-álgebra de sucesos es por defecto P(E).
Si E es un conjunto infinito no numerable como R ó R- o subconjuntos suyos en forma de intervalos, entenderemos que la s-álgebra asociada es la mencionada en el ejemplo anterior, es decir, la generada por todos los intervalos abiertos, cerrados o semi-abiertos (lo que incluye en particular a los puntos), y sus uniones finitas. De este modo podremos calcular probabilidades como las de dichos intervalos.