TEMA 7: MODELOS DE REGRESIÓN
Capitulo 2: Regresión Lineal entre dos variables. Análisis Exploratorio
Coeficiente de Correlación
Supongamos que se diseña un experimento para verificar
la ley de Arrhenius que relaciona linealmente el
logaritmo de la velocidad 
de reacción con la inversa 
(estandarizada) de la temperatura. Se relacionan las dos medidas según los
datos siguientes:
 |
 |
| -3 |  |
| -2 |  |
| -1 |  |
| 0 |  |
| 1 |  |
| 2 |  |
| 3 |  |
|
|
Resulta
Con lo cual,
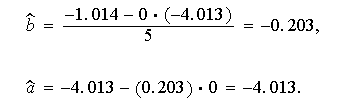
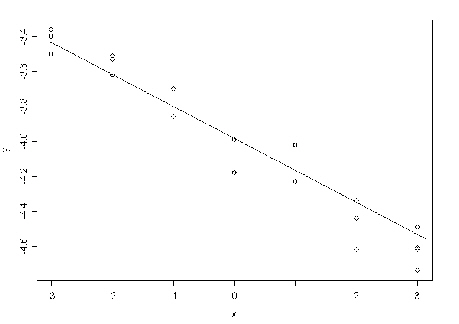
Luego la recta de mínimos cuadrados es
Obsérvese que la pendiente de la recta es negativa.
Hay una forma más intuitiva de describir la pendiente de la recta de mínimos
cuadrados. La pendiente de la recta es el incremento en 
dividido por el incremento en 
;
se asocian distancias entre variables aleatorias, a desviaciones típicas, por
lo que escribimos
La constante de proporcionalidad 
se denomina coeficiente de correlación entre 
e 
y, naturalmente, es igual a
Mide lo cerca que quedan los puntos de una línea recta. Se comprueba que si
todos los puntos quedan justamente en una recta, r
es
1 ó -1 (dependiendo de si la correlación es positiva o negativa). En otro caso está
entre ambos valores.
