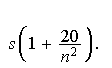TEMA 6: INFERENCIA PARA MEDIAS. MODELOS NORMALES

Capitulo 8: Caso en que 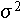$\sigma ^{2}$ es desconocida

Debemos introducir un proceso para aprender también sobre $\sigma ^{2}.$ Formalmente, tenemos

MATH

Modelizamos una distribución a priori MATH y se calcula la distribución a posteriori

MATH

y si, por ejemplo, nos interesa sólo la inferencia respecto a $\mu ,$ empleamos

MATH

    El modelo normal, que es más complicado, puede verse en Lee (1997): Bayesian Statistics. An Introduction y en Gelman et al. (1995): Bayesian Data Analysis. Se utiliza el modelo normal-gamma inversa y conduce a una distribución t de Student con $\left( n-1\right) $ grados de libertad. Cuando $n$ es grande ($n\geq 50$) la distribución t de Student se aproxima a la normal, de aquí se sigue la aproximación propuesta.

    En las aplicaciones que siguen, procederemos (basándonos en la Ley Fuerte de los Grandes Números) del siguiente modo:

Para $n$ suficientemente grande ($n\geq 30$), se sustituye $\sigma ^{2}$ por $s^{2}$ (ó $\sigma $ por $s$) y se procede como antes.

para $n<30,$ MATH suele subestimar MATH y se emplea la correcciónMATH

Ir al indice del capitulo  Ir al apartado siguiente