TEMA 5: INFERENCIA SOBRE PROPORCIONES

Capitulo 6: Comparación de Proporciones.

Se estudia, ahora, el problema de la comparación entre dos proporciones. Para ello se consideran dos poblaciones, que dan lugar a dos experimentos cada uno con una proporción ( $p_{1}$ y $p_{2}$ ) de éxito. Deseamos proporcionar información que permita comparar $p_{1}$ y $p_{2},$ por ejemplo, que sugiere si $p_{1}\geq p_{2}$ o viceversa.

El método que se emplea coincide con el ya utilizado: se multiplica la verosimilitud por la distribución a priori para obtener la distribución a posteriori.

Suponemos que se tiene una muestra de tamaño $n_{1}$ de la primera población con $x_{1}$ éxitos. La verosimilitud es, en este caso,

Además, tomaremos una muestra de tamaño $n_{2}$ de la segunda población con $x_{2}$ éxitos. La verosimilitud es, en este caso,

Para nuestro propósito debemos combinar ambas verosimilitudes. Supondremos que hay independencia entre ambas muestras (a veces esta hipótesis no sea adecuada, como ocurre, por ejemplo, en muestras apareadas), con lo cual la verosimilitud conjunta será el producto de las verosimilitudes marginales

Para cada $p_{i}$ disponemos de información a priori que modelizamos mediante una distribución Supondremos que las $p_{i}$ son independientes. De nuevo esta hipótesis no será siempre adecuada; por ejemplo, podemos creer que si una proporción es grande, es probable que la otra también lo será, o, a la inversa, al ser un proporción grande, la otra será pequeña. Así, la distribución a priori conjunta es (no se incluye, en lo que sigue, las constantes de integración, poniéndose todas las expresiones en función de $\propto$ ):

Calculamos la distribución a posteriori de $p_{1}$ y $p_{2}$ quedando

Se comprueba, además, que

MATH

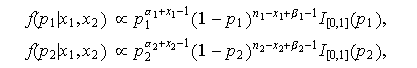
con lo que $p_{1}$ y $p_{2}$ son también independientes a posteriori. Este resultado es, de hecho, general: