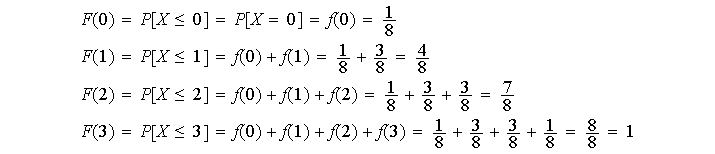TEMA 4: VARIABLES ALEATORIAS

Si son todos los valores admisibles de la v.a. , entonces la suma de las probabilidades de todos los posibles valores de la variable es 1.

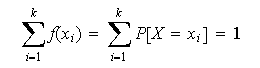
y además todas las probabilidades son no negativas:

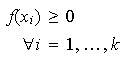
Es evidente que si tenemos tres constantes , los sucesos y son mutuamente excluyentes, es decir, luego . Por ello, si se define se tiene que

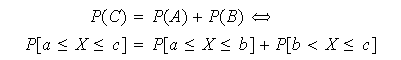
Otro concepto importante es el de función de distribución de una variable aleatoria discreta, , que se define de modo que si es igual a la probabilidad de que tome un valor inferior o igual a :

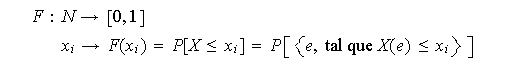
Esta función se representa gráficamente del mismo modo que la distribución de frecuencias relativas acumuladas. Volviendo al ejemplo de las tres monedas, se tiene que

Se observa que a valores no admisibles de la variable aleatoria les pueden corresponder valores de no nulos. Por ejemplo,

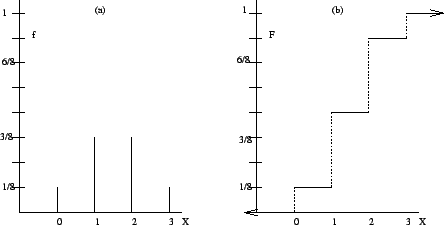
Figura: Función de masa de probabilidad a la izquierda, y función de distribución a la derecha de una v.a. discreta

Es sencillo comprobar las siguientes propiedades de la función de distribución: