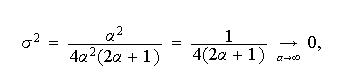TEMA 4: VARIABLES ALEATORIAS
Capitulo 3: Variables Aleatorias Continuas. Distribuciones Continuas
La Distribución Beta. Definición
Una
v.a. tiene distribución beta de parámetros 
en ![$\left[ 0,1\right] $](Tema5__76.png){kind=small}
(y se representa como 
), con 
si su función de densidad es
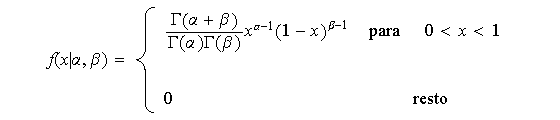
Los momentos de la distribución son
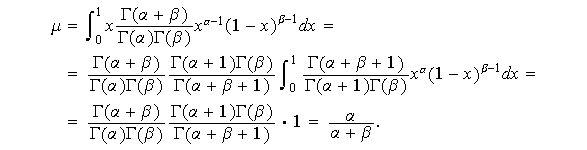
Del mismo modo se demuestra que
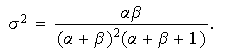
Se recuerda que la función gamma se define como
y su propiedad básica es que
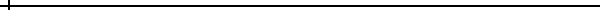
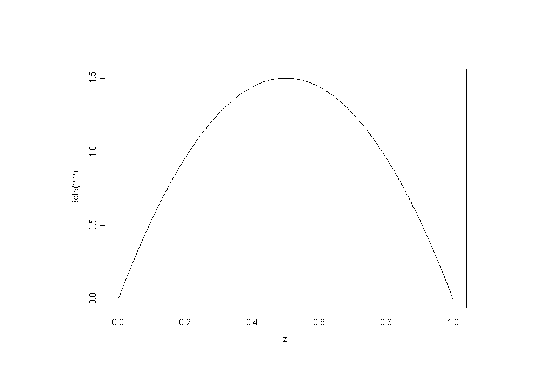
Forma de la Distribución Beta.
En los siguientes ejemplos se muestra la flexibilidad de la familia de distribuciones beta.
 |
Cuando |
|
En general, cuando
Cuando
|
|
Cuando |
|
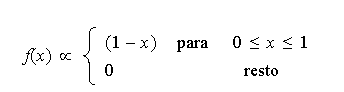
Cuando |
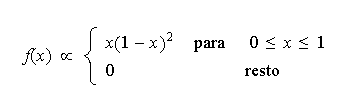
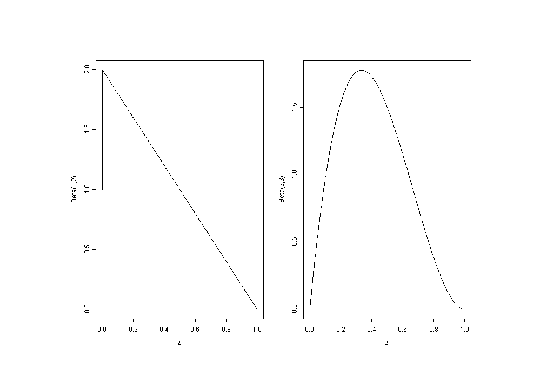
Así, cuando 
se da más importancia a las proporciones menores que 
Recíprocamente, cuando 
se da más importancia a las proporciones mayores que 