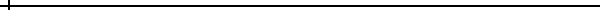TEMA 4: VARIABLES ALEATORIAS
Capitulo 4: Distribuciones Conjuntas
Distribuciones Discretas Multivariantes.
Supongamos que se estudia las caídas de
un sistema, que pueden ser de tres tipos (0, 1, 2), bajo dos modos de operación
(0, 1). Se dispone de las probabilidades de tipo (
)
de caída del sistema, bajo el modo (
)
de operación indicado, en un día, que se expresa en la siguiente tabla.
|
|
|||||
| 0 | 1 | 2 | |||
 |
0 | 0.1 | 0.4 | 0.1 | 0.6 |
| 1 | 0.2 | 0.2 | 0 | 0.4 | |
| 0.3 | 0.6 | 0.1 | 1 | ||
Así, se tiene que 
La tabla define la distribución conjunta
de 
mediante su función de masa de probabilidad.
A partir de ella podemos definir diversas distribuciones de interés. Por
ejemplo, se pueden definir:
 |
La distribución marginal de |
|
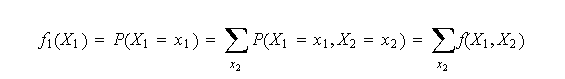
La marginal de |
|
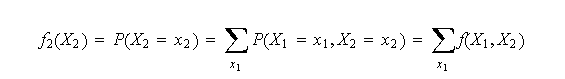
La distribución de |
|
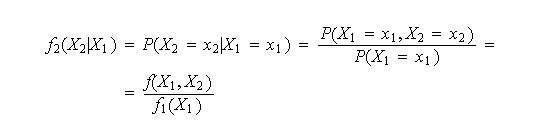
La distribución de |
|
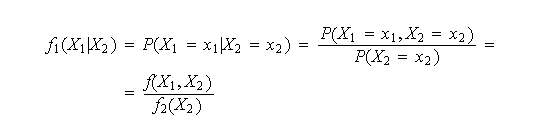
Se dice que |
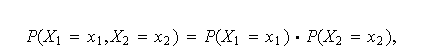
para x1
y x2
cualesquiera, o equivalentemente,
