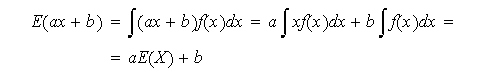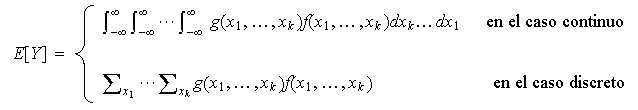TEMA 4: VARIABLES ALEATORIAS
Capitulo 4: Distribuciones Conjuntas
Propiedades del Operador Esperanza. La Covarianza
Si 
entonces
|
|
|
|
En particular, si definimos
se tiene que 
y 
Las definiciones se extienden al caso multivariante. Para 
se tiene que
|
|
Un caso particular es
La esperanza de 
es
se llama covarianza y es una medida de la relación de
crecimiento conjunto de ambas variables. Cuando toma valor positivo es porque
predominan valores de 
grandes a la vez, o ambos pequeños a la vez. Cuando es negativo, resulta que 
es grande y 
pequeño a la vez, o a la inversa.
En el caso de independencia se tiene
En efecto,
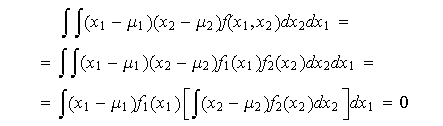
Otros casos importantes son
Se prueba fácilmente que
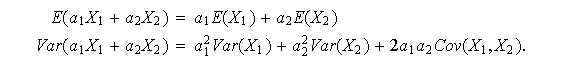
Cuando 
son independientes resulta
y los resultados se extienden a 
variables aleatorias.
