TEMA 4: VARIABLES ALEATORIAS

    Se presentan ahora los conceptos básicos sobre variables aleatorias continuas. Se repiten las mismas ideas que en el caso discreto, con funciones de densidad en lugar de funciones de masa e integrales en lugar de sumas.

    En numerosos experimentos, los resultados podrán ser valores en un conjunto continuo; por ejemplo, si estamos midiendo tiempos de ejecución de trabajos, las mediciones serían valores en el intervalo Para motivar las ideas, supongamos que se ha producido la caída de un sistema en el intervalo En ausencia de información adicional parece razonable sugerir que la probabilidad de que la caída se produzca en un intervalo de duración es De hecho, si designa al suceso ``caída en el intervalo (conjunto) '', se tiene

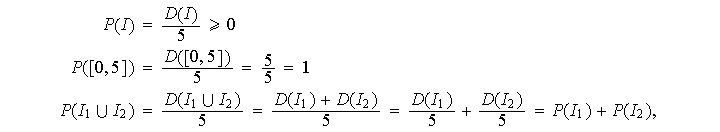
para intervalos no solapantes.

Se observa que para un punto (o un instante), la probabilidad de que la caída se produzca en ese instante es 0.

En el ejemplo anterior, de hecho, se tiene que

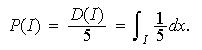
    En el caso de las variables aleatorias discretas, si una variable toma los valores , la probabilidad de que al hacer un experimento, tome uno de esos valores es 1, de modo que cada posible valor contribuye con una cantidad al total:

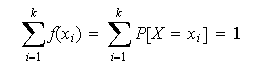
Aún cuando la variable tome un número infinito de valores, no hay ningún problema en comprobar que cada contribuye con una cantidad al total de modo que

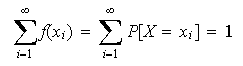
    Sin embargo, cuando la variable es continua, no tiene sentido hacer una suma de las probabilidades de cada uno de los términos en el sentido anterior, ya que el conjunto de valores que puede tomar la variable es no numerable.

        En este caso, lo que generaliza de modo natural el concepto de suma es el de integral. Por otro lado, para variables continuas no tiene interés hablar de la probabilidad de que ya que ésta debe de valer siempre 0, para que la suma infinita no numerable de las probabilidades de todos los valores de la variable no sea infinita.

    De este modo, es necesario introducir un nuevo concepto que sustituya en v.a. continuas, al de función de probabilidad de una v.a. discreta. Este concepto es el de función de densidad de una v.a. continua, que se define como una función , integrable no negativa sobre la recta real, que verifica las dos propiedades siguientes:

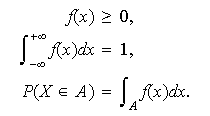
Así, dados , se tiene que

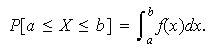
Se puede observar que, por ser una función integrable, la probabilidad de un punto es nula:

y por ello, calcular la probabilidad de un intervalo no afecta nada el que éste sea abierto o cerrado por cualquiera de sus extremos, pues estos son puntos y por tanto de probabilidad nula: