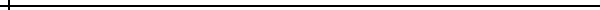TEMA 9: INTRODUCCIÓN AL CONTROL ESTADÍSTICO DE LA CALIDAD
Capitulo 4: Gráficos de Control para mediciones.
Cuando estudiamos mediciones es
habitual intentar controlar la calidad media del proceso, así como su
variabilidad. El primer objetivo se obtiene representando las medias de muestras
periódicas en un gráfico de control de medias (o grafico
). La variabilidad se controla representando los rangos o las desviaciones
típicas,
hablándose, respectivamente, de gráfico R o gráfico s.
Si se conociesen m
y s
y fuese razonable tratar las mediciones como provinietes de una población
normal, podemos decir que, con probabilidad (1 - a),
estará entre
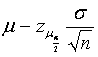
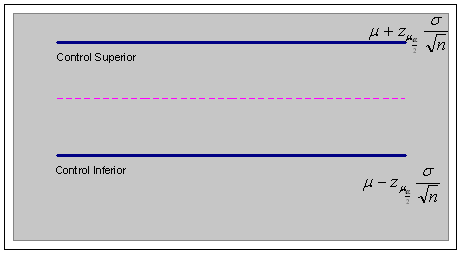
con lo que tendríamos una herramienta grafica para determinar si el proceso está o no bajo control.
En la práctica, m
y s
suelen ser desconocidos y deben estimarse a partir de datos, mientras el proceso
esta bajo control. Por ello, y por no haber garantías de que los datos vengan
de una población normal, se opta por una solución conservadora, sustituyendo 3
a
: con limites 3s,
usualmente estaremos bastante confiados en que no declararemos que el proceso
está fuera de control, cuando, de hecho, esta bajo control.
Si hay muchos datos, m
y s
pueden estimarse casi sin error y la línea central del gráfico
viene dado por la estimación de m
y las líneas superiores por
en el caso no informativo,
Si hay pocos datos, es habitual
agrupar los resultados de 20 o 25 muestras consecutivas cuando el proceso está
bajo control. Si se usan k muestras, cada una de tamaño n, designaremos la
media de la muestra i-esima mediante
y la media de medias:
Como los tamaños maestrales en gráficos de
controlo suelen ser pequeños, suele haber poca perdida de eficiencia la estimar
s
a partir de rangos maestrales, por lo que usaremos el estadístico:
Teniendo en cuenta la distribución de
, tenemos que un gráfico de control
viene dado por:
donde A2 viene dado en la tabla del Apéndice.
Además debemos controlar la
variabilidad del proceso. Observamos que una forma de detectar mayor
variabilidad es a traves de posibles mayores fluctuaciones de
...
Suele emplearse sin embargo, un gráfico (R o s) para controlar la variabilidad, adicionalmente. Los gráficos que se emplean se resumen definen en el siguiente apartado.
